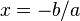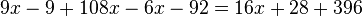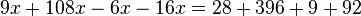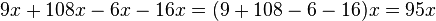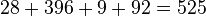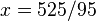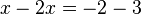ECUACIONES DE PRIMER GRADO
Se dice que una ecuación polinomial es de primer grado cuando la variable (aquí representada por la letra x) no está elevada a ninguna potencia, es decir que su exponente es 1.
Las ecuaciones de primer grado tienen la forma canónica:
ax + b = 0
-
con a diferente de cero.
Su solución es sencilla: 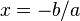
Resolución de ecuaciones de primer grado
Las ecuaciones polinómicas de primer grado se resuelven en tres pasos: transposición, simplificación y despeje, desarrollados a continuación mediante un ejemplo.
Dada la ecuación:
-
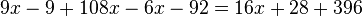
Primero se agrupan todos los
monomios que incluyen la incógnita
x en uno de los miembros de la ecuación, normalmente en el izquierdo; y todos los términos independientes (los que no tienen x) en el otro miembro. Podemos hacerlo teniendo en cuenta que:
- Si sumamos (o restamos) un mismo monomio en los dos miembros, la igualdad no varía.
En términos coloquiales, decimos: si un término está sumando (como 16x en el miembro de la derecha) pasa al otro lado restando (−16x a la izquierda); y si está restando (como el −9 de la izquierda), pasa al otro lado sumando (+9 a la derecha)
La ecuación quedará entonces así:
-
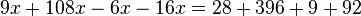
Como puede verse, todos los términos que poseen la variable x han quedado en el primer miembro (a la izquierda del signo igual), y los que no la poseen, por ser sólo constantes numéricas, han quedado a la derecha.
Simplificación
El siguiente paso es convertir la ecuación en otra equivalente más simple y corta.
Realizamos la simplificación del primer miembro:
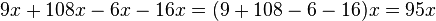
Y simplificamos el segundo miembro:
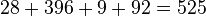
La ecuación simplificada será:
-

Despeje
Ahora es cuando llegamos al objetivo final: que la incógnita quede aislada en un miembro de la igualdad. Para lo cual recordamos que:
- Si multiplicamos o dividimos por un mismo monomio (o número) a los dos miembros, la igualdad no varía.
En términos coloquiales: Para despejar la x, si un número la está multiplicando (Ej: 5x) se lo pasa al otro lado dividiendo (n/5) sin cambiar su signo. Y si un número la está dividiendo (Ej: x/2), entonces se lo pasa al otro lado multiplicando (n×2) sin cambiar su signo.
En la ecuación debemos entonces pasar el número 95 al otro miembro y, como estaba multiplicando, lo hará dividiendo, sin cambiar de signo:
-
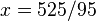
Se comprueba que el ejercicio está teóricamente resuelto, ya que tenemos una igualdad en la que x equivale al número 525/95. Sin embargo, debemos simplificar.
Resolvemos la fracción (numerador dividido entre denominador) en caso de que el resultado diera exacto; si diera decimal, simplificamos la fracción y ése es el resultado.
En la ecuación, vemos que el resultado de la fracción es decimal (525:95 = 5,5263157894737)
Por tanto, simplificando, la solución es:
-

Ejemplo de problema
Pongamos el siguiente problema: el número de canicas que tengo, más tres, es igual al doble de las canicas que tengo, menos dos. ¿Cuántas canicas tengo? El primer paso para resolver este problema es expresar el enunciado como una ecuación:

Donde x es la incógnita: ¿cuántas canicas tengo?
La ecuación se podría leer así: El número de canicas que tengo, más tres que me dan, es igual al doble de mis canicas, quitándome dos.
El enunciado está expresado, pero no podemos ver claramente cuál es el valor de x; para ello se sigue este procedimiento: Primero se pasan todos los términos que dependen de x al primer miembro y los términos independientes al segundo. Para ello tenemos en cuenta que cualquier término que se cambia de miembro cambia también de signo. Así obtenemos:
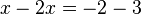
Que, simplificado, resulta:
- x = - 5
Esta expresión nos lleva a una regla muy importante del álgebra, que dice que si modificamos igualmente ambos miembros de una ecuación, el resultado es el mismo. Esto significa que podemos sumar, restar, multiplicar, dividir, elevar y radicar los dos miembros de la ecuación por el mismo número, sin que ésta sufra cambios. En este caso, si multiplicamos ambos miembros por -1 obtendremos:
x = - 5
El problema está resuelto.